signaturebta.blogg.se

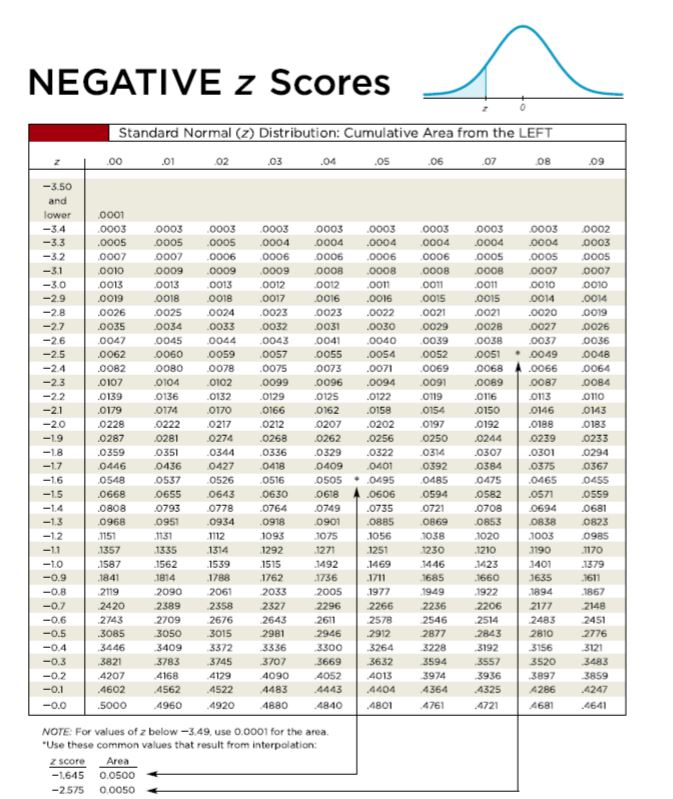
Consider a chemistry class with a set of test scores that is normally distributed. Z-scores can be used in situations with a normal distribution.

A z-score converts a data value and standardizes it so that we are able to determine how many standard deviations a specific data value will lie above or below the mean. The calculation does not appear so straightforward but as it turns out we can use a z-score for situations such as this. This calculation was possible since $49,000 was exactly one standard deviation away from the mean.Ĭonsider a salary which does not lie exactly one, two or three standard deviations from the mean, such as $38,500. In turn, using the 68-95-99.7 Rule we can determine that a salary of $49,000 is higher than 84% of the other salaries for this segment of the economy.

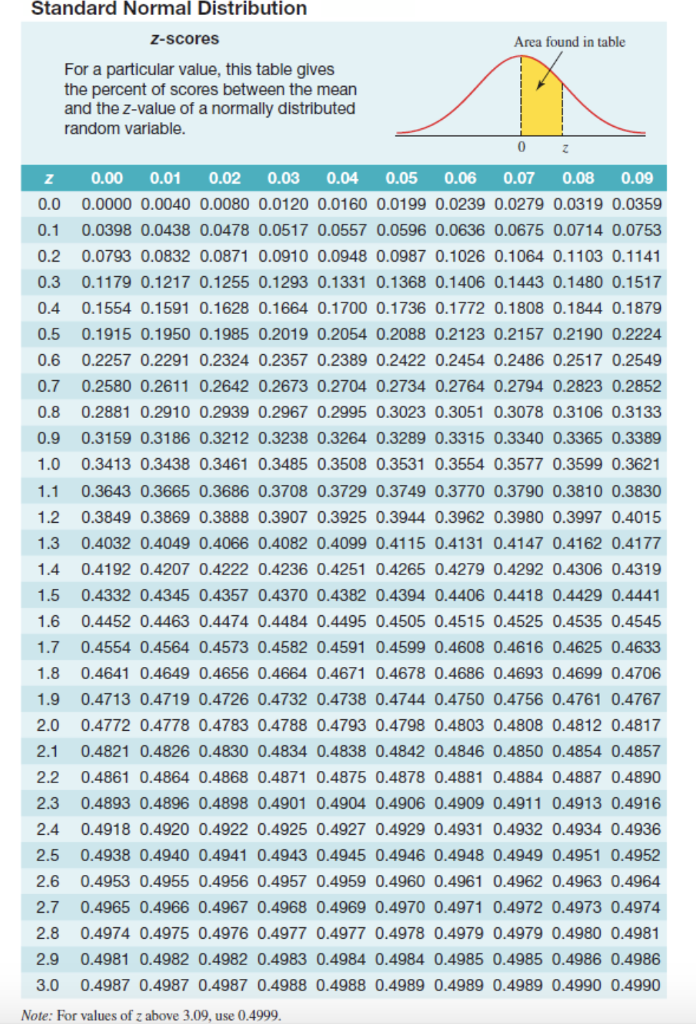
With this information we are able to determine that a salary of $49,000 lies exactly one standard deviation above the mean since $45,000 + $4000 = $49, 000. Acertain segment of the economy has a normally distributed salary, with a mean salary of $45,000 and a standard deviation of $4000. Reconsider an example from the previous section. When a data set is normally distributed we can use a standardized score, called the z-score, to determine the number of standard deviations that a data value is from the mean.